Алгоритм Брезенхема для регулирования мощности

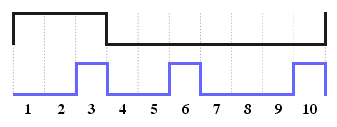
Регулирование напряжения микроконтроллером

При создании микроконтроллерных устройств периодически возникает задача регулирования некой аналоговой величины, например, напряжения на выводе МК, яркости светодиода, мощности нагревательного элемента, и т.д. и т.п. Для формирования аналогового сигнала с заданной амплитудой на выводах МК часто используется метод широтно-импульсной модуляции - ШИМ. Вдаваться в теорию работы ШИМа не стану, в Сети все давно прекрасно описано. В основе ШИМ лежит подача на выход МК импульсов с изменяемой скважностью, чем выше скважность D (отношение длительности импульса к его периоду), тем выше будет амплитуда сигнала после пропусканияимпульсов через интегрирующую RC-цепочку:

Достоинством ШИМа является простота его реализации - большинство современных МК имеют аппаратную поддержку ШИМ. Но возможны ситуации, в которых ШИМ не дает желаемого результата. Например, в случае, если надо управлять яркостью свечения светодиода. Вот как будут выглядеть ШИМ-диаграммы для разных яркостей:

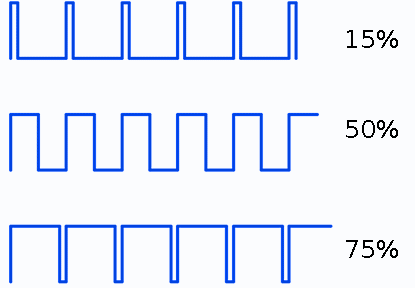
На каждой итерации ШИМ дает единичный положительный импульс, длительность которого пропорциональна яркости. В результате светодиод начинает быстро мигать, и поскольку импульсы подаются с относительно высокой частотой, а наше зрение инертно, мы воспринимаем это мерцание как непрерывное свечение. Частота мерцания равна частоте ШИМа и в случае малых яркостей и не слишком высоких частот оно может стать заметным для глаза. Чтобы и избавиться от него необходимо увеличивать частоту ШИМ, что не всегда возможно. Например, в случае, когда требуется рулить не единичным светодиодом, а большим светодиодным дисплеем с динамической индикацией, или в случае, когда надо регулировать мощность нагрузки привязываясь к полупериодам сетевого напряжения, как в случае с регулятором мощности паяльника.

Вторым способом уменьшения мерцания является изменение формы управляющего напряжения. Т.е., вместо одного большого импульса подавать серию более коротких импульсов той же самой суммарной длительности и равномерно распределённых по интервалу.

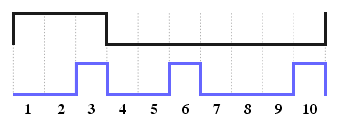
Каким образом можно выполнить равномерное распределение импульсов по всему интервалу? Поиск в Сети дает ответ - надо использовать алгоритм Брезенхэма. Алгоритм Брезенхэма - это алгоритм, использующийся в машинной графике для рисования прямых линий.. Но причем же тут наша задача о равномерном заполнении интервала импульсами?!

Алгоритм Брезенхема

А вот причем. Пусть нам надо равномерно распределить M импульсов (яркость) по N ячейкам. Давайте нарисуем прямую линию в декартовой системе координат. По оси X будем откладывать время (0 .. N-1), по оси Y прямая будет достигать величины M. Т.е., возвращаясь к искомой задаче, для яркости 100% (M = N) прямая будет идти под углом 45 градусов, для яркости равной нулю прямая будет совпадать с осью X.

Размер сетки: 10 x 10 20 x 20 30 x 30 40 x 40 50 x 50 60 x 60 70 x 70 80 x 80 90 x 90 100 x 100
Наклон прямой: 0 % 10 % 20 % 30 % 40 % 50 % 60 % 70 % 80 % 90 % 100 %

Внимательно посмотрев на этот график уже можно увидеть наши равномерно распределённые импульсы. В самом деле, чем больше яркость, тем выше поднимется кривая и тем больше будет переходов. Теперь продифференцируем нашу прямую - значениям X, в которых величина Y увеличивается на 1 будет соответствовать 1, остальным значениям - 0.

Дискретность: 10 20 30 40 50 60 70 80 90 100
Яркость: 0 % 10 % 20 % 30 % 40 % 50 % 60 % 70 % 80 % 90 % 100 %

Осталось разобраться с алгоритмом. Рисование линии реализуется псевдокодом:

function line(x0, x1, y0, y1)
     int deltax := abs(x1 - x0)
     int deltay := abs(y1 - y0)
     int error := 0
     int deltaerr := deltay
     int y := y0
     for x from x0 to x1
         plot(x,y)
         error := error + deltaerr
         if 2 * error >= deltax
             y := y - 1
             error := error - deltax

Добавляя вычисление разности с предыдущим значением, получаем диаграмму импульсов:

uint8_t bresenham_data[10];
void calcBresenham(uint8_t size, uint8_t brightness) {
  size--;
  brightness--;
  int error = size - brightness;
  uint8_t x = 0;
  uint8_t y = 0;
  uint8_t prevY = 1;
  while ( x <= size ) {
    const int error2 = error * 2;
    bool value = y != prevY;
    bresenham_data[x] = value;
    prevY = y;
    if ( error2 > -brightness ) {
      error -= brightness;
      x++;
    }
    if ( error2< size ) {
      error += size;
      y++;
    }
  }
}

Затем, эту функцию можно еще упростить переписав как:

void calcBresenham(uint8_t size, uint8_t brightness) {
  int16_t error = size - brightness;
  uint8_t x;
  for (x = 0; x < size; x++) {
    if ( error < size/2 ) {
      error += size;
      bresenham_data[x] = 1;
    } else {
      bresenham_data[x] = 0;
    }
    error -= brightness;
  }
}

Наконец, мо жно ещё немного изменить алгоритм и оформить его в виде библиотечного файла:

typedef struct bresenham_struct {
  uint8_t size;
  uint8_t value;
  int16_t error;
  uint8_t stepNumber;
} bresenham_struct;

void bresenham_init(struct bresenham_struct *st, uint8_t size) {
  st->size = size;
}

void bresenham_setValue(struct bresenham_struct *st, uint8_t val) {
  st->stepNumber = 0;
  st->value = val;
  st->error = st->size/2;
}

bool bresenham_getNext(struct bresenham_struct *st) {
  bool result;
  st->error -= st->value;
  if ( st->error < 0 ) {
    st->error += st->size;
    result = true;
  } else {
    result = false;
  }
  if ( ++st->stepNumber >= st->size) {
    st->stepNumber = 0;
    st->error = st->size/2;
  }
  return result;
}

Тут структура bresenham_struct хранит информацию о настройках и текущем состоянии генератора последовательности Брезенхэма;
Метод bresenham_init(st, size) вызывается в момент инициализации и задаёт количество разбиений оси времени (количество градаций яркости);
Метод bresenham_setValue(st, value) вызывается для задания яркости. Например, если size = 100, то яркость может быть от 0..99;
Метод bresenham_getNext(st) вызывается периодически по прерыванию таймера (или любым другим способом) и возвращает true, если надо подать положительный импульс и false в противном случае.

Результат работы последнего алгоритма можно увидеть ниже:

Дискретность: 10 20 30 40 50 60 70 80 90 100
Яркость: 0 % 10 % 20 % 30 % 40 % 50 % 60 % 70 % 80 % 90 % 100 %

По ссылкам ниже можно скачать файл с реализацией алгоритма (для AVR GCC) и файл с тестов, проверяющих валидность генерируемых последовательностей.

Файлы:
bres_test.c - тесты
bresenham.h - библиотечный файл